Matemática para Engenheiros: Espiral de Arquimedes, Fermat, etc..

Engenheiros, Arquitetos, Designers, Programadores, Inventores, Curiosos..adoradores da matemática

Sabemos que na história da humanidade, os engenheiros são os fazedores de coisas, a eles damos o crédito das grandes obras. Não necessariamente só os que passam pela academia se tornam bons criadores, muitos engenheiros atualmente conseguem o seu bacharel sem aprenderam quase nada de matemática, muitos sem vocação para os cálculos, empurram o curso na velha metodologia do decoreba, esses certamente nada grandioso irão criar, faltar-lhe-ão as bases, se você é como eu que sente falta do conhecimento mais aprofundado para realizar os seus projetos, aqui é o seu lugar.

O blog foi inspirado no livro "Ensinar e estudar Matemática em Engenharia", de Jorge André.

De que Matemática particular precisam os estudantes de Engenharia? Há uma Matemática específica para engenheiros? O que tem de especial o ensino da Matemática para estudantes de Engenharia?

Não existe Engenharia sem Matemática, e a boa preparação matemática ajuda muito o futuro engenheiro de concepção, de projeto, de desenvolvimento, de inovação, de investigação.

Não se constroe e nem se cria nada sem a matemática, nem mesmo uma costureira é capaz de fazer uma roupa sem antes fazer um cálculo, embora usando uma metodologia mais simples, uma boa costureiranecessita conhecer bastante de geometria para criar um molde bem alinhado as formas do corpo proporcionando o bom caimento do tecido, é uma geometria altamente complexa que envolve cônicas, engenharia de superfícies curvas,a mesma lógica para construir um prédio, uma antena, tem que calcular, medir..claro que tem variáveis a mais como o vento, a resistência do concreto, etc..a roupa precisa apenas vestir bem. Os primeiros alfaiates certamente eram bons matemáticos, assim como os bons pintores e escultores antigos.

Você sabe qual o papel da Matemática na formação educacional de um futuro engenheiro? Poucos tem a compreensão lúcida e informada da natureza da Matemática como ciência do pensamento rigoroso, e da forma por que ela se aplica, bem como das diversas modalidades da ação

Uma das principais “forças” da Matemática está em que as suas ideias e ferramentas são gerais, e muito do poder da Matemática, mesmo da elementar, vem-lhe precisamente da aplicabilidade de ideias gerais em vários contextos diferentes.

O rigor do pensamento matemático tende a ir ao fundo de tudo, mas no ensino da Engenharia não há tempo para isso, nem a motivação dos estudantes será em geral suficiente para grandes aprofundamentos.

No livro o autor faz análises sobre a “simbiose formativa” da Matemática com a Física e a Engenharia, e sobre a capacidade de dar “saltos lógicos” como pré-requisito essencial na modelação de fenómenos naturais e na posterior aplicação prática dos resultados do respectivo tratamento matemático.

Trata-se de uma obra de reflexão crítica original e profunda sobre um tema de capital importância para o futuro da Engenharia, num país que pretende manter-se tecnologicamente atualizado e com os recursos humanos indispensáveis à sua modernização.

Os problemas diferentes exigem tipos diferentes de conhecimento e perícia em engenharia e tecnologia.

O Brasil não tem patentes, embora a população seja extremamente criativa, empreendedora, mas falta-lhe mais conhecimento lógico- matemático, a medida que avançamos na educação poderemos fazer as transformações necessárias para o desenvolvimento.

terça-feira, 17 de maio de 2011

Espiral de Arquimedes, Fermat, etc..

Excelente material, uma relíquia do tempo que o artista era exageradamente ligado a matemática, a perfeição das suas criações.

"A matemática aplicada é tão importante para a arquitetura que, se a matemática não tivesse sido inventada, os arquitetos teriam sido obrigados a inventá-la." by Mario Salvadori

O que é um Rosette logarítmica?

são características comuns dos pavimentos da época romana até o Renascimento, e têm sido bem documentados por Kim Williams.

Em geral, apresentam uma série de círculos concêntricos e outras curvas cuja distância do centro da roseta continuamente aumentos, as interseções formando um número de triângulos curvilíneos cujo tamanho aumenta com a sua distância do centro da roseta. Essas curvas são geralmente outros arcos de circunferência que não são concêntricos com o centro da roseta. Mas, ocasionalmente, vemos uma roseta em que uma curva como uma espiral logarítmica, a qual chamamos de uma roseta logarítmica.

O que é uma espiral logarítmica?

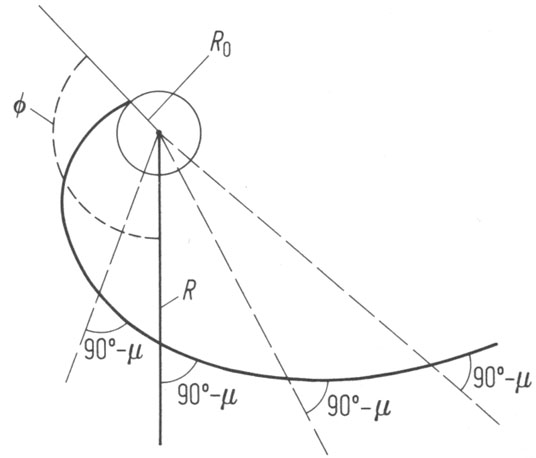
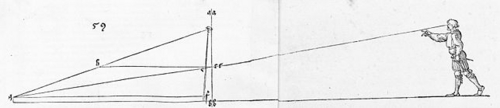
mostra um gráfico polar de uma porção NPQ de uma espiral logarítmica. A espiral logarítmica é uma curva plana cuja vetorial ângulo q é proporcional ao logaritmo do comprimento r do raio vetor OP .
Esta espiral foi descoberta pelo matemático francês René Descartes em 1638. Ele é visto na natureza no Nautilus câmaras, chifres de animais, e algumas plantas. No século 19 o matemático Bernoulli descobriu que o ângulo f entre a tangente T à espiral em qualquer ponto P eo vetor raio OP a esse ponto não muda como a espiral cresce (Figura 2). Daí a espiral logarítmica é também chamada deespiral equiângulo . Pode ter sido essa propriedade de manter sua forma que solicitado Bernoulli chamá-lo de Spira mirabilis ou espiral milagrosa

É útil comparar a espiral logarítmica para o círculo. O c Ircle intersecta a sua própria raios em toda a parte o mesmo ângulo de 90 °, enquanto a espiral logarítmica intersecta a sua própria raios em todos os lugares no mesmo ângulo, que pode variar de 90 °.

Aa equação da espiral em forma polar é

um q r = ln

onde um é uma constante. Reescrevendo esta equação exponencial em [3] dá a forma

r = e um q

Para incrementos iguais de q = 1, 2, 3,. . ., Os nossos valores de r são:

e um , e 2a , e 3a . . .

ou,

e um , (e um ) 2 , (e um ) 3 . . .

Nós reconhecemos isso como uma progressão geométrica com razão comum e um . Assim, em uma espiral logarítmica, os vetores de raio r , por incrementos iguais do ângulo polar q formam uma progressão geométrica. Por outro lado, se os vetores de raio para uma forma curva de uma progressão geométrica de incrementos iguais do ângulo polar, a curva é uma espiral logarítmica .

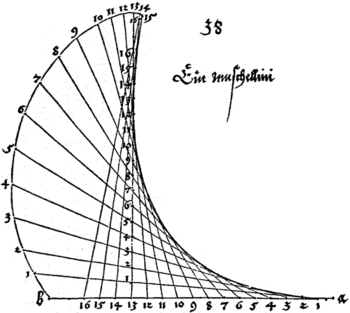
Voltando à nossa construção na Figura 5 , vamos

OA r = 1 , OB = r 2 , OC = r 3 , etc .

Os raios r 1 e r 2 são os dois lados do triângulo OAB . Vamos denotar a relação de r 2 para r 1 pela letra k.

r 2 / r 1 = k

ou,

r 2 = kr 1

Aqui k é uma constante cujo valor depende de nossas escolhas iniciais dos raios do círculo interno e da altura da primeira banda.Agora triângulo OBC é semelhante ao triângulo OAB , e desde que as dimensões correspondentes de figuras semelhantes são proporcionais, podemos escrever,

r 3 r / 2 k =

r 3 kr = 2 k = (kr 1 ) = k 2 r 1

Além disso, triângulo OCD é semelhante ao triângulo OAB , então,

r 4 kr = 3 k = (k 2 r 1 ) = k 3 r 1

e assim por diante. Nossos raios, por incrementos iguais de ângulo, formando assim a progressão geométrica

r 1 , kr 1 , k 2 r 1 , k 3 r 1 , ...

provando que os pontos A, B, C, D,. . . mentir sobre uma espiral logarítmica.

Os segmentos de reta ligando estes pontos não, claro, mentir sobre a espiral, mas dá sua localização aproximada. Se queremos uma roseta logarítmica com triângulos curvilíneos , que colocava a roseta em metal ou madeira fina, como mostrado acima, e ligar os vértices dos triângulos com curvas suaves. As bases dos triângulos curvilíneos seria arcos circulares concêntricos com o centro da roseta. Tal formato pode ser cortado e os pedaços usados como modelos para as peças individuais.